Teorema de Pitágoras: rompecabezas de Perigal

En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Si os fijáis en la imagen anterior, según el teorema de Pitágoras, el área del cuadrado que tiene como lado la hipotenusa (c²) tiene que ser igual a la suma de las áreas de los cuadrados que se forman tomando como lados los catetos (a² y b²). Por si tenéis alguna duda el área de un cuadrado es igual a lado por lado, o sea, al lado al cuadrado.

Por lo tanto, demostrando que se cumple la relación existente entre las áreas de los cuadrados quedará demostrado el teorema de Pitágoras.

Al matemático inglés Henry Perigal (1801/1898), se le atribuye una ingeniosa comprobación del teorema:

"Sobre el mayor de los cuadrados construidos sobre los catetos se determina el centro y se trazan dos rectas paralela y perpendicular a la hipotenusa del triángulo. Con las cuatro piezas obtenidas más el cuadrado construido sobre el otro cateto podemos cubrir el cuadrado construido sobre la hipotenusa."

Compruébalo de forma manipulativa haciendo clic en la siguiente imagen.

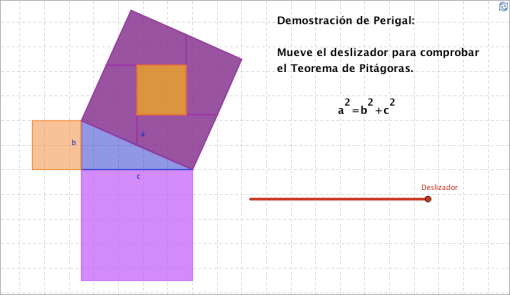
(por Inmaculada Gijón Cardos - elblogdeinma.wordpress.com)

En el siguiente enlace podéis ver muchas más demostraciones del teorema de Pitágoras. Visitar