MatemáticasIES Antonio Menárguez Costa: Cuadrados mágicos

Un cuadrado mágico es un conjunto de números naturales dispuestos en una matriz cuadrada de tal forma que la suma de los números por columnas, filas y diagonales principales sea la misma, la constante mágica.

Generalmente, en un cuadrado de n x n (n² casillas) se sitúan todos los números del 1 al n². Como podéis ver en la imagen anterior, un cuadrado mágico de 3 x 3 tiene 9 casillas; en ellas se han dispuesto todos los números del 1 al 9.

Los cuadrados mágicos se conocían ya en la antigua China, sobre el tercer milenio a.C.. También otras civilizaciones como los indios, los egipcios, los árabes y los griegos tuvieron constancia de su existencia. Generalmente, en todas estas civilizaciones se les atribuían propiedades místicas.

La entrada de los cuadrados mágicos en Europa se sitúa sobre el siglo XIV. El grabado Melancolía (1514) de Alberto Durero (Núremberg, 1471), se caracteriza, como muchas de sus obras, por su iconografía compleja y su simbolismo. En este grabado aparece un cuadrado mágico de 4 x 4 cuya constante mágica es 34, valor que se obtiene al sumar cualquiera de sus filas, de sus columnas, o alguna de las dos diagonales principales.

Pero, además, sus cuatros esquinas suman 34, los cuatro número centrales suman 34, los cuatro números centrales de las filas superior e inferior suman 34, al igual que los cuatro números centrales de las columnas izquierda y derecha. Si dividimos el cuadrado en cuatro cuadrados tenemos que los números que integran cada uno de ellos suman 34. Los números 3, 8, 14 y 9 (movimiento del caballo de ajedrez a partir del 3) suman 34 al igual que el 2, 5, 15 y 12. Y si reemplazamos cada número por su cuadrado o por su cubo obtenemos otros dos cuadrados que aunque no son mágicos también tienen propiedades interesantes. En los dos números centrales de la fila inferior aparece reflejada la fecha de la obra, 1514.

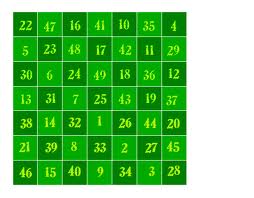
Como veis algunos cuadrados mágicos pueden llegar a ser bastante complejos. Aquí tenéis uno de 7 x 7.